Dengan menggunakan konsep dan sifat harga mutlak, kita bisa mengaplikasikannya dalam perhitungan integral tertentu.

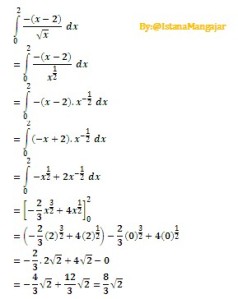

*Semoga Bermanfaat*
Soal dan Pembahasan Pertidaksamaan Harga Mutlak (1-3)
Harga Mutlak didefinisikan sebagai sebuah
notasi yang menyatakan nilai yang selalu positif. Suatu fungsi yang
berada dalam kurung harga mutlak selalu bernilai positif dan tidak
mungkin negatif.
Sifat-sifat utama harga mutlak dalam sebuah pertidaksamaan adalah:
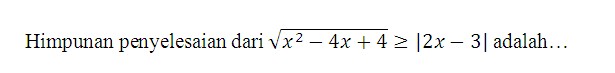
Penyelesaian:
Jadi HP nya = 1 ≤ x ≤ 5/3
2.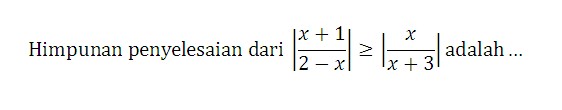
Penyelesaian:
Menggunakan aturan Pertidaksamaan Harga Mutlak, Pertidaksamaan Pecahan dan Pertidaksamaan Suku Banyak.

 Jadi HP nya = x ≥ -1/2
Jadi HP nya = x ≥ -1/2
3.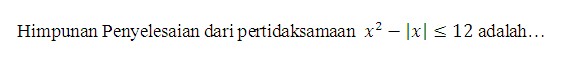
Penyelesaian:

Sifat-sifat utama harga mutlak dalam sebuah pertidaksamaan adalah:
- |x| = x, jika x ≥ 0
- |x| = -x, jika x < 0
- Jika |x| < p maka himpunan penyelesaiannya -p < x < p, p > 0
- Jika |x| > p maka himpunan penyelesaiannya x < -p atau x > p, p>0
- Jika |f(x)| < p maka himpunan penyelesaiannya -p < f(x) < p, p > 0
- Jika |f(x)| > p maka himpunan penyelesaiannya f(x) < -p atau f(x) > p, p>0
- Jika |f(x)|<|g(x)| maka ekuivalen dengan [f(x)]² < [g(x)]²
- Jika |f(x)|>|g(x)| maka ekuivalen dengan [f(x)]² > [g(x)]²
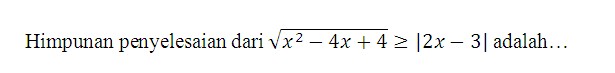
Penyelesaian:

Jadi HP nya = 1 ≤ x ≤ 5/3
2.
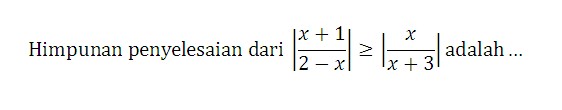
Penyelesaian:
Menggunakan aturan Pertidaksamaan Harga Mutlak, Pertidaksamaan Pecahan dan Pertidaksamaan Suku Banyak.

 Jadi HP nya = x ≥ -1/2
Jadi HP nya = x ≥ -1/23.
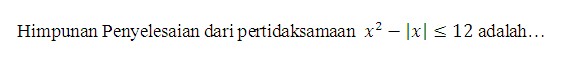
Penyelesaian:


0 komentar:
Posting Komentar